Tlak v kapalinách

• Působí-li síla o velikosti $F$ kolmo na plochu o obsahu $S$, vyvolá uvnitř tekutiny tlak definovány vztahem $p=\frac{F}{S}$
• Kde:
  • $p$ - tlak ($Pa$)
  • $F$ - síla ($Na$)
  • $S$ - obsah($m²$)

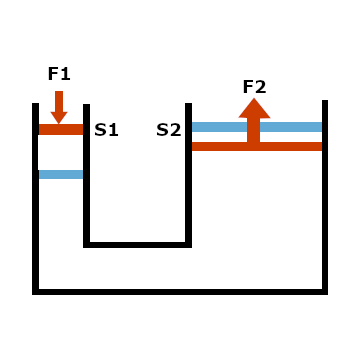
Tlak vyvolaný vnější silou

• Využití nestlačitelnosti
• $∆V = S1_(V1) = S2_(V2)$
• $\frac{F1}{S1} = \frac{F2}{S2}$

Příklad 1

• Tlak oleje v hydraulickém lisu je $20 Mpa$. Obsah plochy většího pístu je $15 dm²$.
• Jaká je síla, která zvedá píst?
• $F = p * S = 20 000 000 * 0,15 = 3 000 000 N$

Příklad 2

• Rameno autojeřábu se musí zvedat silou 40 kN . Zvedá ho píst o obsahu 200 cm².
• Jaký tlak musí vydržet přívodní hadice?
• $p = \frac{F}{S} = \frac{40 000}{0.02} = 2 MPa$
• Jaký musí být obsah pístu olejové pumpičky, když na něj motor působí silou 1000N ?
• $S = \frac{F}{p} = \frac{1000}{2 000 000} = 5 * 10^{-1}m² = 5cm²$

Příklad 3

• Myš o hmotnosti 200 g chce zvednout slona o hmotnosti 6 tun
• Jaký obsah musí mít velký píst, když malý píst s myší má obsah 100 cm² ?
• $S_2 = F_2S_1/F1 = 6000 x 0,01 / 2 = 300 m²$

Příklad 4

• Obsahy průřezů válců hydraulického lisu jsou 20 cm² a 800 cm². Na menší píst působí síla o velikosti 100 N.
• Určete:
  • Tlak, který tato síla vyvolá v kapalině
  • Velikost tlakové síly působící na větší píst
  • Dráhu o kterou se posune větší píst, jestliže se menší píst posune o 8 cm
  • Práci kterou při tomto posunutí vykoná tlaková síla
• Tlak vyvolaný v kapalině: $p = \frac{F_1}{S_1} = \frac{100}{2*10(-3)} Pa = 50 kPa$
• Síla na větším pístu: $ F_2 = F_1\cdot\frac{S_2}{S_1} = 100 \cdot \frac{8\cdot10-2}{2\cdot10-3} = 4 kN $
• Posun většího pístu: $∆V = S1_(s1) = S2_(s2) , s2= s1 * \frac{S1}{S2}, s2 = 8*10-2 * \frac{2x10-3}{8x10-2} m = 2 mm$